
noticed by now that complex numbers sometimes appear in Mathematica's output. As far as I know the only way to close a figure window is using plt.close(fig) as described above. Make a x2+2x-3 plot of f over a valid domain in the positive real numbers. Note that even del fig will not close the associated figure window. This call is equivalent to plt.clf() only if fig is the current figure. I'll assume in the following that fig is an instance of a Figure:įig.clf() clears the entire figure. methods of the Figure classĪdditionally, the Figure class provides methods for clearing figures. Furthermore, there is the syntax close('all'), which closes all figures. If no argument is given to close(), the currently active window will be closed. The argument can either be a number or name given to a window when it was created using figure(number_or_name) or it can be a figure instance fig obtained, i.e., using fig = figure(). The close() function furthermore allows one to specify which window should be closed. Which functions suits you best depends thus on your use-case. Plt.close() closes a window, which will be the current window, if not specified otherwise. Plt.clf() clears the entire current figure with all its axes, but leaves the window opened, such that it may be reused for other plots. the currently active axes in the current figure.
In this case, there are three different commands that remove stuff:
I here assume that pyplot has been imported as import matplotlib.pyplot as plt. The above no longer works in Mathematica version 10. Pyplot is a module that collects a couple of functions that allow matplotlib to be used in a functional manner. The Wolfram Language has many ways to plot functions and data. Additionally, there are functions from the pyplot interface and there are methods on the Figure class. Its innovative approach also offers insights into areas too often neglected in a student treatment, including complex chaos, mathematical art, physics in three or more dimensions, and advanced fluid dynamics. They all do different things, since matplotlib uses a hierarchical order in which a figure window contains a figure which may consist of many axes. This book presents complex numbers in a state-of-the-art computational environment. Easiest is probably to just generate them with ContourPlot instead of MeshFunctions. I haven't thought of a good way to get the mesh lines to vary in color. (*turn off axes, because I don't like them with frames*) (*hue according to argument, with shift so arg(z)=0 is red*) (*turn off scaling so we can do computations with the actual complex values*) PlotPoints -> 50, MaxRecursion -> 0, Mesh -> 50, (*color and mesh functions don't trigger refinement, so just use a big grid*) (*just need a vis function that will allow x and y to be in the color function*) Of course, Michael Trott wrote the Mathematica guide books, which contain many beautiful graphics, but seem to have fallen behind the accelerated Mathematica release schedule!
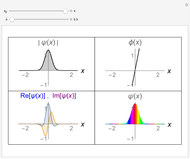
The Return of Riemann surfaces (updates for Mma v6) Visualizing Riemann surfaces of algebraic functions, IIa, IIb, IIc, IId. Not that this should stop you from giving your favourite approach that uses a lower level construction!Įdit: There were some nice articles by Michael Trott in the Mathematica journal on: I know that there are other ways to visualize complex functions – such as the "neat example" in the Plot3D docs, but that's not what I want.Īlso, I do have one solution below (that has actually been used to generate some graphics used in Wikipedia), but it defines a fairly low level function, and I think that it should be possible with a high level function like ContourPlot or DensityPlot. Note that this is not a problem with Plot3D where all 3 parameters (x,y,z) get passed to ColorFunction. But the problem is in both types of plots, ColorFunction only takes a single variable equal to the contour or density at the point – so it seems impossible to make it colour the phase/argument while plotting the absolute value. In the Mathematica documentation page Functions Of Complex Variables it says that you can visualize complex functions using ContourPlot and DensityPlot "potentially coloring by phase". Hampton of Neutral Drifts) of the zeta function with overlayed contours of absolute value: Wolfram Knowledgebase Curated computable knowledge powering Wolfram|Alpha.How can I make a Mathematica graphics that copies the behaviour of complex_plot in sage? i.e. Wolfram is often called a search engine for solving problems. Wolfram Universal Deployment System Instant deployment across cloud, desktop, mobile, and more. Wolfram Data Framework Semantic framework for real-world data.


 0 kommentar(er)
0 kommentar(er)
